Global flood astronomical date range

---

NOTE: (reprinted with permission from the author from CreationScienceHallofFame.org)

---

Dr. Walt Brown, nearly three months ago, announced an astronomical fix for the Global Flood. When he did that, he provoked the precise sort of debate scientists ought to have. Brown, with his customary boldness, challenged anyone who doubted him: “Check my math!” Dr. Matthew Jachimstahl, a skeptic (both of the Hydroplate Theory and of the Bible), accepted Brown’s challenge. Brown recently released the full results of that challenge.

A range of dates for the Global Flood

Your correspondent has copies of all the correspondence between Drs. Brown and Jachimstahl. (In fact, that correspondence began early in July, after Dr. Brown revised his results earlier.) The result of that debate does not change Dr. Brown’s value for the most likely date of the Global Flood. But it does change the standard deviation of that value. The new standard deviation is 100 years. Thus the range of most likely dates for the Global Flood are the year 3290 BC, give or take 100 years.

During the Brown-Jachimstahl correspondence, Brown realized that an independence assumption buried in a standard statistical formula he was using didn’t hold for his comet data. Certain numbers were dependent upon each other. Also, the published “orbital periods” (the time it takes a comet to complete one complete orbit) are not true orbital periods. Instead, they are the periods for osculating orbits.

An osculating orbit (literally, “kissing orbit”) is the orbit an object might follow at any time, if all possible perturbing influences on that object were to disappear. No object follows an osculating orbit, least of all a comet. But osculating periods are the easiest to work with. Changes in osculating orbits and their elements reflect the influences other objects have on them.

But “analytical” solutions still exist to answer the question, “How far off might one be in predicting a closest approach to the sun by projecting any comet’s course backward in time?” Brown explains all his methods at: https://www.creationscience.com/onlinebook/TechnicalNotes2.html.

How to back-calculate the Global Flood

As ever, Dr. Walt Brown’s Hydroplate Theory says all comets, asteroids, and meteoroids formed at the same time. They formed, furthermore, from water, rock and mud that the Global Flood event launched into space. That launch, of course, happened when “the fountains of the great deep broke open” (Genesis 7:11) in a hypersonic water jet.

Brown used two comets, from the 2008 Catalogue of Cometary Orbits, having these features:

• Long orbital periods
• High inclinations to the plane of the ecliptic (the orbit of earth around the sun)
• Actual records of apparitions (“appearances” of the comets) stretching back at least two thousand years.
• Hundreds of available perihelia, either actual or simulated.

(See Table 1.)

Table 1

Comet	Earliest known perihelion		q	i
	Recorded	Simulated
Halley	239 BC	1403.80 BC	0.586 AU	162.3°
Swift-Tuttle	68 BC	702.30 BC	0.9595 AU	113.45°

[the table is continued below...]

Comet	Earliest known period	N	Expected error, as σ, to predict
			Next Period	Launch Date
Halley	69.86 years	27	1.56 years	130 years
Swift-Tuttle	129.33 years	20	2.98 years	159 years

Here, q is the perihelion distance, i is the inclination, and N is the number of periods from the earliest recorded or simulated period, back to the eventual launch date. An AU, or “astronomical unit,” is the average distance of earth from the sun.

The simulated perihelia come from detailed studies of Comets Halley and Swift-Tuttle from the team under Dr. Donald Yeomans. He published these findings separately in the Monthly Notices of the Royal Astronomical Society.

These two studies are part of the first of four steps to arrive at the last result. Briefly, they are:

1. Calculate the standard deviation for the change-of-period for each comet. This is the “expected error to predict next period” in the table.
2. For each year between 4000 and 6000 years before the present day, compute the sum of squares of the differences between the Julian date at the beginning of the year, and the date of the nearest expected perihelion of each comet. The year in which that sum-of-squares is the least, is the year those comets were closest to earth at the same time.
3. Try that again, except start back-stepping from a random point in history for each comet, instead of the earliest known or simulated perihelion. Most desktop computers can do this a million times with ease.
4. Now calculate the standard deviation of a normal or Gaussian distribution around that date.

Three ways to define the range of dates for the Global Flood

Walt Brown listed three ways to arrive at the breadth of the date range:

The geometric method is the classic one. For any N, the total error works out to:

\[ \sigma \sqrt{(N)2+(N-1)2 +(N-2)2+...+(3)2+(2)2+1} \]

Or:

\[ \sigma \sqrt{\frac{N(N+1)(2N+1)} {6}} \]

This formula, for each of the two comets, gives the values in the “Expected error to predict launch date” column. The reciprocal of the square of the combined error is the sum of the reciprocals of the squares of the individual errors. That result is 100 years.

Brown also lists the algebraic and Monte-Carlo methods to find this error. All three methods give the same answer: 100 years.

How remarkable is this date range for the Global Flood?

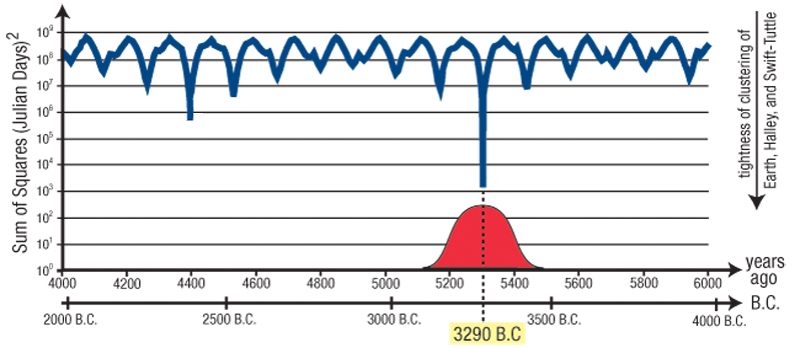
This graph (Fig. 1) (from Brown’s Technical Notes) shows how remarkable the middle of the Global Flood date range is. It is a semi-log plot showing the sum-of-squares of the differences in time of the perihelia of the two comets from any given date, as a function of years before present. This plot forms several downward spikes at somewhat regular intervals. But at 3290 BC, the spike extends significantly lower than average.

Figure 1

The deepest spike points to the most likely date range for the Global Flood. Dr. Jachimstahl raised another issue: why search between 4,000 years and 6,000 years before the present? Why not go as far back as a million years? Might not similar tight convergences happen at regular intervals, perhaps 12,000 years apart?

But in proposing that, Dr. Jachimstahl ignored a fundamental fact about comets. They die. When a comet no longer displays its plumage on its approach to the sun, or displays so little of it that we on earth cannot see it anymore, we say that comet is dead. The problem: comets that come within one AU or closer to the sun, die after a hundred close passes.

The earliest known period for Comet Halley (see the table) is 69.86 years. Thus if Comet Halley was older than about 7,000 years, it would be dead today. But in its last apparition (1986), it showed its plumage as brightly as it did in 1066, when Londoners stared at it in shock and awe shortly before William the Conqueror really showed them what shock and awe felt like.

So the best place to search for a common launch date of the material that became the comets, must fall within the interval of the longest possible life of the comet with the shorter period. If that comet is “alive” today, then one cannot search back to a time before said comet was “born.”

To do otherwise, one must further assume that the Oort cloud exists, and that Comets Halley and Swift-Tuttle both fell out of it. But the Oort cloud has a deal-killer already: too many comets making their closest approach to the sun at less than 3.0 A.U. Including both Comets Halley and Swift-Tuttle. That holds also for comets having short periods, on the order of those for Halley and Swift-Tuttle. (This table compares the Hydroplate Theory to all other theories of where comets came from, and lists all deal-killers.)

What this means for Bible scholarship

This correspondent calculated twenty-four possible dates for the Global Flood, based on alternative theories for:

• The chronology of the Kings of Israel and Judah following Solomon’s reign,
• The chronology of the Sojourn in Egypt,
• The chronology of the life of Terah, father of Abraham, and
• The use of three different manuscript sources of the ages of the Patriarchs.

Five of the twenty-four dates for the Global Flood fall within the two-hundred-year range 3290 BC ± 100 years.

• All five are consistent with the long chronology of the Sojourn in Egypt.
• Four of the five are consistent with the Septuagint (LXX), and one with the Samaritan Pentateuch (SP), for the ages of the post-Global Flood patriarchs when each sired his next named son.
• Three of the five are consistent with the long chronology for the birth of Abraham.
• Three of the five (though not the same three) are consistent with the Ussher/Lloyd chronology of the Kings of Israel and Judah.

The most remote of these five dates (3343 BC) still falls well within this range, at 3290 BC plus about one-half sigma before then.