Faster than Light - part 2

By

Joe Spears MS
Astronomy
Physics
Cosmology
Setterfield

NOTE on terminology: CDK implies that light was faster in the past, and then over time, gradually decayed. So, CDK refers to the DeKay (decay) of C (the speed of light): CDK.

This article is a continuation of the article Faster than light? 1  which explores the possibility of the speed of light being faster in the past.

In the article Distant Starlight in a Young Universe: Attempted Solutions, 2 astrophysicist Jason Lisle, PhD, considers CDK or the idea that the speed of light was faster in the past and decayed over time. He presents 3 arguments against CDK, all of which are refuted below. 

Below I shall explain why and how those 3 arguments fail to disprove/refute the Setterfield decay model of the speed of light.

Argument 1 - Supernova SN1987A

Explanation

First, Lisle said, regarding a supernova discovered in 1987:

... only a small fraction of the light from this explosion was directed toward the earth. Some light went off in other directions and reflected off of the surrounding gas which then redirected the light toward earth – a “light echo.”  This light arrived after 1987 because it took time to go from the supernova to the surrounding gas.  By measuring the distance between the supernova and the surrounding gas, and dividing by the time between the two events, we can compute the speed of light when the supernova happened.  And we find it is consistent with the current value of c ... 2

What is missed here is that the result is also consistent with CDK! This calculation is based on some implicit assumptions which are not valid. 

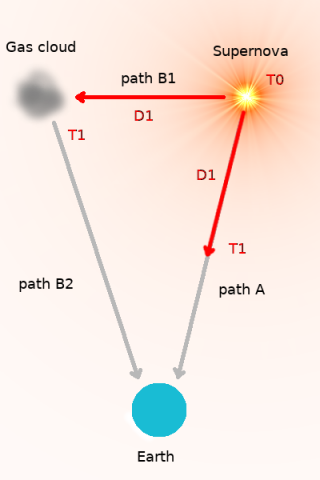
The calculation Lisle performed is simple. It is based on 2 paths of light from the supernova. One path is directly from the supernova to earth. This path is path A in Figure 1.

Light paths at T1
Figure 1

The other path is from the supernova to a cloud of gas, from which the light is reflected to earth. This is path B. Notice that path B is composed of 2 parts: path B1 and path B2.

In the caption to an image in Lisle's article, 2 he said the following: (emphasis added) 

These light echos show that the speed of light perpendicular to our line of sight was the same at the time and distance of the supernova as here and now. 2

This implies that the distance between the earth and the gas cloud is the same as the distance from the earth to the supernova. 3

Lisle took the time interval between the time of detection of the supernova and the time of detection of light from the gas cloud, and divided that into the distance between the supernova and the gas cloud (path B1) to get the speed of light along path B1. We shall see this was actually not a measurement of the speed of light along path B1!

Now, of course, it took time for light to travel from the gas cloud to earth (path B2 of Fig. 1). The time Lisle used in his calculation was not the time interval between the time point of the  supernova explosion and the time point of the appearance of light from the gas cloud on earth; rather, Lisle used the time point of the (later!) appearance of light on earth from the supernova in 1987 as the starting point of the time interval used in his calculation.

These were the only two time points used in deriving the time duration used in Lisle's calculation as shown in Figure 2:

  1. the time point of arrival of light on earth from the supernova, T2 (not the actual time of the explosion)
  2. the time point of arrival of light on earth from the gas cloud, T3

Key Point

Light travels the same distance along two different paths during the same time interval. This would be true even if the speed of light varied during this time period, as long as the speed varied in the same way along both paths, so that the speed of light was the same on both paths at any specific instant of time. This is the case per CDK. CDK means light speed changes, over time - not through space! Therefore the speed of light, even with CDK, is the same at any same specific time on different paths. 4

So, in the ensuing analysis, we shall see light traveling differing paths, during the same time period, with the result being that identical distance is covered on both paths during that time period.

Light paths at T2
Figure 2

Light would decay at the same rate regardless of position or location. CDK is not a function of distance nor of position, but is a function of time. This means the speed of light would be the same on all paths in the diagrams at the same times. Even if light was continuously decaying nonlinearly, the distance covered on any path between two time points would be the same as the distance covered on another path during the same time period.

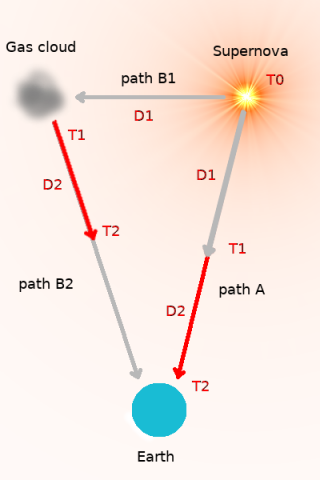
Referring to Fig. 1, we see that at time T0 the supernova exploded. Light then later arrived at the gas cloud at time T1. During this time, from T0 to T1, light not only traveled the distance D1 between the supernova and the gas cloud, but light also traveled the same distance, D1, from the supernova toward earth. The distances D1 on paths B1 and A are equal. They are distances light traveled during the same time period.

Now, consider Figure 2. D2 is the remaining distance along path A to earth directly from the supernova after time point T1. Continuing in time from T1 to T2, light traveled from the gas cloud toward earth (on path B2). The identical time period occurred along path A between time point T1 and time point T2, so the same distance (D2) was covered on both path A and path B2. We noted earlier that the distance to earth from the gas cloud (path B2) and the distance from the supernova to earth (path A) were the same. (Note that the distance D1 + D2 is the length of path A and would also be the length of path B2.)

The distance from the gas cloud to earth is D1 + D2. We see from Figure 3 that light had traveled from the gas cloud distance D2 toward earth at time point T2. Time point T2 is the time at which light coming directly from the supernova appeared on earth.

Light paths at T3
Figure 3

The length of both paths, from supernova to earth and from gas cloud to earth, were the same and equal to D1 + D2. Therefore, at time point T2, the remaining distance for light to travel to earth from the gas cloud, D3, has to equal D1. The time of arrival of light on earth from the gas cloud was T3. This tells us that between T2 and T3, light traveled the distance D1. During this time, light’s speed was the modern value, since T2 is the modern 1987 and T3 was later.

What Lisle calculated was the distance D1 divided by the time interval between T2 and T3. These are the distance and the time that light traveled, respectively, starting in 1987! There is no wonder that the result was the 1987 value. This calculation was not the calculation of the speed of light during the ancient past, while light was traveling between the supernova and the gas cloud.

Another Perspective

Lisle assumed the time interval between T2 and T3 was the time that light took to travel between supernova and gas cloud, i.e., distance D1. We have seen that D1 is the actual distance light traveled between T2 and T3. However, that was during modern times, along the path between earth and gas cloud. To assume it took the same time to travel that distance in ancient times is to assume the same speed in ancient times, i.e., implicitly assuming what was to be proved, which is logically invalid.

Lisle implicitly assumed distance D3 was the same as D1, which is true. The error was in assuming that the time light took to travel D3 was the same as the time light took to travel D1. This is true only if the speed of light in the past was the modern value. Thus, Lisle in this calculation implicitly assumed what was to be proved, which is invalid.

Argument 2: Redshift - Wrong Assumption About Frequency

Lisle says,

Second, since light is a wave, any change in its speed over time will result in a change in frequency. 2

This is not true! It is false, specifically, in the case for which wavelength is not constant. 

The simple equation for this is v = fw, or f = v/w, where f is frequency, w is wavelength, and v is speed (velocity). To see this, consider that f, frequency, is the number of waves per second, or a number divided by time. Then consider that multiplying f by the length of a wave gives a number times a length divided by total time. This result is speed!

Anyway, per the equation, 

f = v/w

or

f = c / w

where c is made the velocity, we see that a change in c (speed of light) requires a change of frequency only if wavelength is constant. We can change c in this equation all we want, without changing frequency, by simply changing w.

Therefore, CDK is not ruled out by asserting that CDK requires a change in frequency. Wavelength could change instead of frequency. It is hypothetically possible that the wavelength of a single photon of light did not change, after emission of the photon, while that photon was in transit, but that the wavelength of different, sequentially emitted, photons of light indeed did change over time, while the speed of light changed over time, per CDK as described by Setterfield. This is elaborated with more detail in the article Redshift Quantization Explained  5 (https://tasc-creationscience.org/article/quantized-redshift-explained).

So, Lisle's conclusions are not valid here, being based on a foundation of an invalid starting assumption (that wavelength did not change with c over time).

Argument 3: Conservation of Mass & Energy - Wrong Assumption About Mass

Lisle goes on to say

Third, the speed of light is very special and unlike other speeds.  It essentially sets the relationship between space and time, the relative strengths of magnetic fields to electric fields, and the relationship between matter and energy.  But our very existence depends on these things being essentially constant.  The famous equation E=mc2, for example, shows that the amount of energy contained in a mass is proportional to that mass multiplied by the square of the speed of light.  Therefore, if the speed of light changes, then either the mass or energy (or both) of everything in the universe must also change. 2

This conclusion is also incorrect. This has already been dealt with in the TASC article Does Changing Speed of Light Violate Energy Conservation? 6 There it was shown, including a mathematical derivation, that energy conservation is not violated in the case of a changing speed of light!

Also, I might add, Lisle stated that the speed of light determines "the relative strengths of magnetic fields to electric fields," while I suggest the opposite: namely, that the electrical permittivity of the vacuum \( \epsilon \) and the magnetic permeability of the vacuum \( \mu \) determine the speed of light. 7 In actual fact, these values and the speed of light are related, as per the following equation, in which the speed of light is c, the electrical permittivity of the vacuum is \( \epsilon \), and the magnetic permeability of the vacuum is \( \mu \):

\[ c=\frac{1}{\sqrt{\epsilon\mu}} \]

Equation for speed of light c, in terms of the electrical permittivity of the vacuum and the magnetic permeability of the vacuum

The video at https://www.youtube.com/watch?v=qtqTPCAw7Fo shows the derivation of the above formula for the speed of light from Maxwell's equations and tells us that the speed of light is determined by the 2 values in the equation. These were described in the video as values for a vacuum. However, is space really a vacuum? We know more now than we did around 1905, when Einstein's special theory of relativity appeared. We know there are virtual particles in space, as well as a vacuum energy, also known as ZPE (the Zero Point Energy). We also know that light travels faster through some mediums/materials than it travels through others. Light is slowed by the medium through which it passes, and those virtual particles plus vacuum energy also make up a medium. This medium in the vacuum changed the values for those 2 variables, which in turn resulted in a change in the speed of light.) 

Changes of the vacuum energy and density of virtual particles would result in changes of these two factors, epsilon and mu.

Setterfield explains:

Polarization can only occur if there are charged particles capable of being moved or re-oriented in an electric field. But we are working with what appears to be a vacuum. The conclusion is that the vacuum must contain charged particles, capable of moving, which are not associated with the air. This certainly seems to  indicate the presence of virtual particle pairs which flash into and out of existence so rapidly. Their instantaneous presence,  however, means we have a “polarizable vacuum.” The extent to which the vacuum “permits” itself to be polarized in an  electric field is called the electric permittivity of free space. This permittivity is designated by the Greek letter epsilon written as ε. 8

and

If the ZPE strength increased, then both ε and μ would also increase proportionally as a result of the proportional increase in the number of virtual particle pairs. 9

We see that a changing ZPE would change both ε and μ which in turn would change c. Was the ZPE different in the past than it is now? Evidence that indeed it was different in the past is found in the red shift data. See TASC article Redshift Quantization Explained  10 (https://tasc-creationscience.org/article/quantized-redshift-explained).

Addendum

Also suggesting that faster light in the past is not yet ruled out by creation scientists, the June 2021 presentation by creationist physicist Russell Humphries suggested a faster speed of light in the past. The video of Humphries’s presentation can be viewed at https://www.youtube.com/watch?v=09yngV0c6Y8

Conclusion

If we dig a little deeper, we often can see more. By thinking about the impact of CDK, not just on one path, B1, but on other paths (B2 and A), we can see a different conclusion might be discovered than what appears from a first look.

In Lisle’s article Distant Starlight in a Young Universe: Attempted Solutions, 2 three arguments against CDK were given. They have all been examined above and shown for various reasons to be invalid. As a result, CDK has not been ruled out "as a viable solution to the perceived distant starlight problem," as stated in the article (at least not yet, not by the 3 arguments presented).

In short, CDK remains a viable alternative explanation for the distant starlight problem.